 量子きのこ
量子きのこかばん「サーバルちゃん!5次行列の特殊ユニタリの作り方、別解を見つけたよ!」
サーバル「えっと・・・」
かばん「量子力学における、5状態系の角運動量演算子の代数を思い出してみて!?」
サーバル「・・・わかんないや!」
かばん「あ、そっか・・・このサーバルちゃんはダイバージェンスが1頭身低い世界線のサーバルちゃんだった・・・。じゃあこれの行列式わかる!?」
サーバル「わかるよ!今計算してみるねー!うーみゃみゃみゃみゃ!みゃぁー!」
p1=[1/4;%i/2;-sqrt(6)/4;-%i/2;1/4]
p2=[1/2;%i/2;0;%i/2;-1/2]
p3=[sqrt(6)/4;0;1/2;0;sqrt(6)/4]
p4=[1/2;-%i/2;0;-%i/2;-1/2]
p5=[1/4;-%i/2;-sqrt(6)/4;%i/2;1/4]
P=[p1,p2,p3,p4,p5]
det(P)
illust/65625209
(13枚目)
scilab
サーバル「マイナス1だよ」
かばん「じゃあ、2列目全体をiで割って、3行目全体の符号を反転して、4行目全体にiをかけたら、行列式はどうなるかな!?」
illust/65625209
(15枚目)
サーバル「うーみゃみゃみゃみゃ!みゃぁー!」
p2=p2/%i
p3=-p3
p4=p4*%i
illust/65625209
(14枚目)
scilab
サーバル「1になったよ!かばんちゃん!」
かばん「ちゃんとユニタリになってるかもう一度確認してみてくれる!?」
サーバル「P-P' おおー!ゼロ行列だよ!すっごーい!」
かばん「おおー!・・・ん?もうサーバルちゃんのドジー^^;それはユニタリ行列じゃなくてエルミート行列の性質でしょ~」
サーバル「ごめんごめん^^;clean(inv(P)-P') ええ!?これもゼロ行列だよ!」
かばん「えええええ!?特殊ユニタリかつエルミートな5次行列なのぉー!?」
???「これが”りょうし”のすごさなのです」
??「なのです」
かばん「博士!それに助手!」
コノハ博士「りょうしのすごさがわかったのなら、さっさとおかわりを作るのです」
ミミ助手「とっととやるのです」
かばん「ちょっと待ってください^^;今これを作ってて」
n=now()-today()
t=1000000n
角度(°)=mod(round(t,0),360)
角度(rad)=角度(°)*PI()/180
mmult(横ベクトル、回転行列)
z=z+下駄
A:ズーム
x=Ax/z
y=Ay/z
x-yの2Dグラフを表示
コノハ博士「なんですかこれは!?」
ミミ助手「ヒトの遺物、Excelなのです」
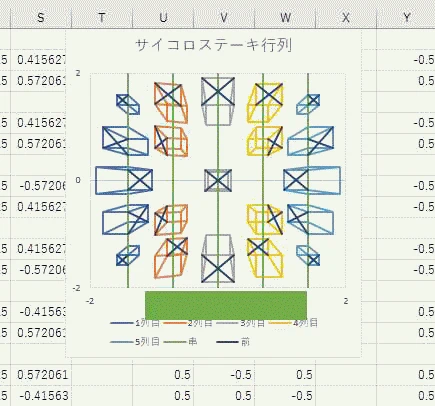
かばん「エルミートかつユニタリな行列の可視化器を作ってまして・・・
5次行列なので、要素が25個あって、固有ベクトルなのを5本の串1本1本に刺さったサイコロステーキで表現してみました。
バツ印のついているほうが向きで、絶対値は、側面の面積で表現しています。
固有ベクトルなので、それぞれの列を串で回転させることができます。
ただし、エルミート行列の固有状態なので、90度ごとにとびとびになってます。
規格化された固有ベクトルなので、サイコロステーキ串1本当たりの1側面の面積の和は5本とも1です」
ミミ助手「じゅるり・・・」
コノハ博士「これが・・・りょうしですか!!!」
サーバル「私はカット役だよ!」
ミミ助手「この計算をサーバルがやったのですか!?」
サーバル「ふっふーん!」
コノハ博士「ヒトの遺物scilabを用いているとはいえ、これだけのルールを扱うとは、サーバル、なかなかやりますね」
ミミ助手「我々と同じくらい賢い素質があるのです」
サーバル「やったー!」
かばん「やったねサーバルちゃん!」
コノハ博士「それにしてもかばんはアホなのです」
かばん「ええ!?」
ミミ助手「なぜExcelで、しかもマクロなしでこれを作ろうと思ったのですか!?労力の無駄遣いです」
かばん「デスヨネー^^;プログラミングがまだ怖くて・・・」
コノハ博士「かばんにも怖いものがあるのですか」
サーバル「大丈夫だよ!フレンズはお友達のためなら怖いものでも克服しちゃうんだから!ほら~」
ミミ助手「サーバル!やめるのです!図書館が!本が!我々の不動産、知的財産が!燃え尽きてしまうのです!!!」
かばん「ギンギツネさん、キタキツネさん!タライさんの出番ですよー!」
ギン「私たちも不動産なら持ってるのにねぇ?」
キタ「持ってないのはセルリアンハンターくらいだよ」
2017-10-28 00:44:53 +0000